6. Численное интегрирование функции

Алиас: интеграл.

Цель работы

На примере разработки программы для численного интегрирования функции с заданной точностью:

• методом прямоугольников;
• методом трапеций.

При выполнении лабораторной работы освоить следующие приемы программирования:

• передачу в функцию параметров "по значению" и "по адресу";
• передачу в функцию имени функции;
• передачу одномерных массивов в функцию;
• объединение разнородных данных в структуру;
• использование массивов из элементов типа структура.

Задание

Вычислить определённый интеграл $\int_{a}^{b} f(x) \,dx$ в пределах от $a$ до $b$ для четырех функций:

• $f_1 = x$;
• $f_2 = \sin(22 x)$;
• $f_3 = x^4$
• $f_4 = \arctan(x)$.

Численное интегрирование функции с заданной точностью выполнить двумя методами:

• метод прямоугольников. Вычисление интеграла оформить в виде функции IntRect;
• метод трапеций. Вычисление интеграла оформить в виде функции IntTrap.

Вычисления выполнить для пяти значений точности: 0.01, 0.001, 0.0001, 0.00001 и 0.000001.

Исследовать быстродействие алгоритма в зависимости от подынтегральной функции и требуемой точности (быстродействие алгоритма можно оценить числом элементарных прямоугольников $n$).

предупреждение

Для выполнения задания использовать $n_{max} < 100000$. В противном случае ваша программа при тестировании будет останавливаться по таймауту, а тест будет считаться провалившимся.

Для каждого метода представить результаты вычислений в виде 5 таблиц, по одной таблице для каждого значения точности. В каждой таблице выводить данные для всех четырех функций.

Для печати таблицы результатов использовать функцию

void PrintTabl(I_print i_prn[], int k)

Здесь i_prn[] – массив структур типа I_print размерностью k.

Функция PrintTabl представлена для программ на C и для программ на Cpp.

предупреждение

Значения a ($a \in \mathbb{Z}$) и b ($b \in \mathbb{Z}$) устанавливается генератором случайных чисел из диапазонов:

• $a \in [0, 1]$;
• $b \in [2, 3]$.

Пример вывода в консоли

Пример вывода для одной точности:

Значение a: 1
Значение b: 3

Метод прямоугольников. eps = 0.01.
+-----------+-----------------+-----------------+---------+
|  Function |     Integral    |      IntSum     |    N    |
+-----------+-----------------+-----------------+---------+
|    y=x    |     0.0000000000|     0.0000000000|        0|
+-----------+-----------------+-----------------+---------+
| y=sin(22x)|     0.0000000000|     0.0000000000|        0|
+-----------+-----------------+-----------------+---------+
|   y=x^4   |     0.0000000000|     0.0000000000|        0|
+-----------+-----------------+-----------------+---------+
| y=arctg(x)|     0.0000000000|     0.0000000000|        0|
+-----------+-----------------+-----------------+---------+

Метод трапеций. eps = 0.01.
+-----------+-----------------+-----------------+---------+
|  Function |     Integral    |      IntSum     |    N    |
+-----------+-----------------+-----------------+---------+
|    y=x    |     0.0000000000|     0.0000000000|        0|
+-----------+-----------------+-----------------+---------+
| y=sin(22x)|     0.0000000000|     0.0000000000|        0|
+-----------+-----------------+-----------------+---------+
|   y=x^4   |     0.0000000000|     0.0000000000|        0|
+-----------+-----------------+-----------------+---------+
| y=arctg(x)|     0.0000000000|     0.0000000000|        0|
+-----------+-----------------+-----------------+---------+

Указания по выполнению работы

Сумма Римана

к сведению

Основано на статье "Riemann sum"

В математике сумма Римана - это определенный вид аппроксимации интеграла конечной суммой. Она названа в честь немецкого математика девятнадцатого века Бернхарда Римана. Одним из очень распространенных применений является аппроксимация площади функций или линий на графике, а также длины кривых и других приближений.

Сумма вычисляется путем разбиения области на формы (прямоугольники, трапеции, параболы или кубики), которые вместе образуют область, аналогичную измеряемой области, затем вычисляется площадь для каждой из этих форм и, наконец, складывается все эти небольшие области вместе. Этот подход может быть использован для нахождения численного приближения для определенного интеграла, даже если фундаментальная теорема исчисления не позволяет легко найти решение в замкнутой форме.

Методы суммирования

Четыре метода суммирования Римана для аппроксимации площади под кривыми:

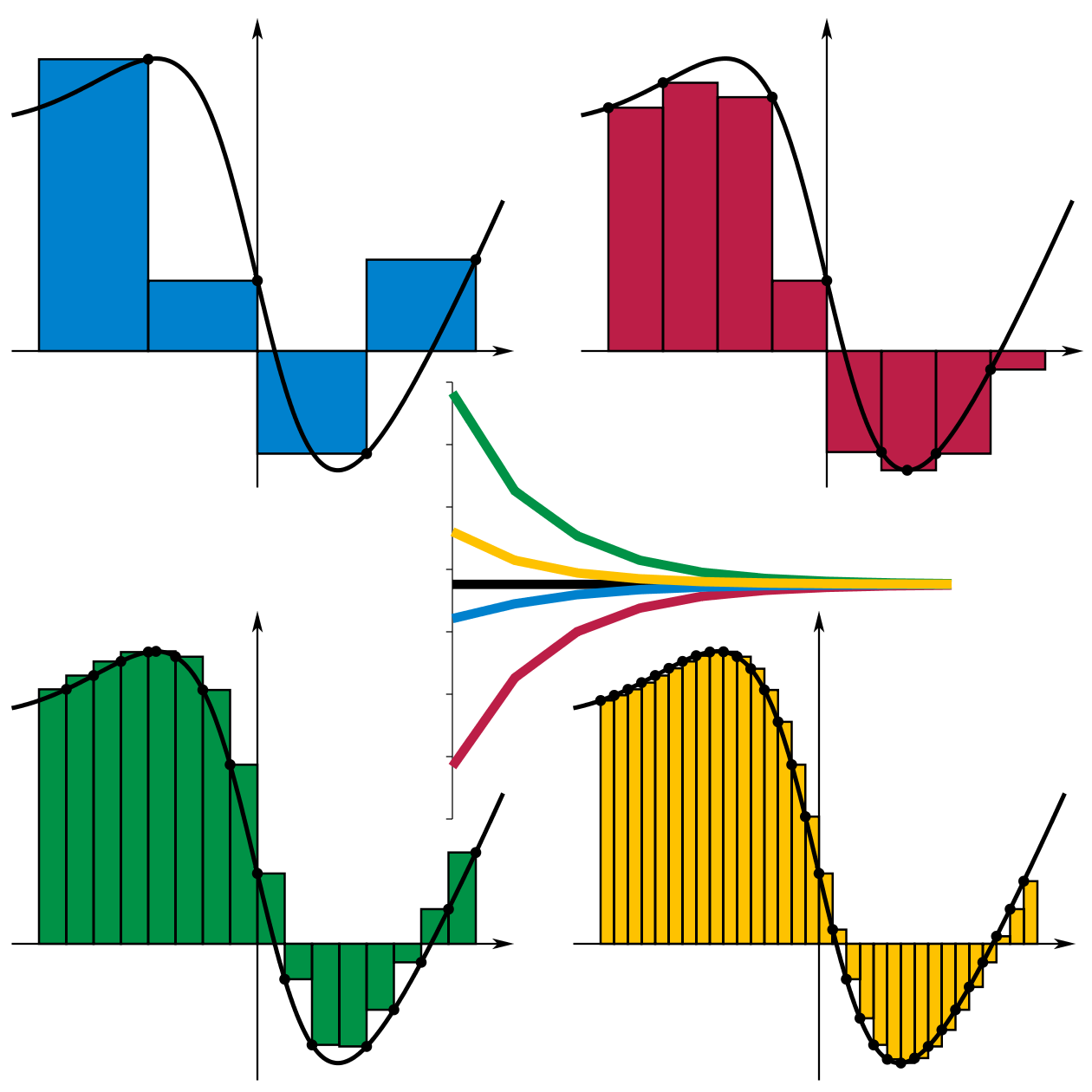
Правый (синяя график) и левый (красный график) методы выполняют аппроксимацию, используя правую и левую конечные точки каждого подинтервала соответственно. Условно можно обозначать их как интегральные суммы Римана.

Методы максимума (зеленый график) и минимума (желтый график) выполняют аппроксимацию с использованием наибольших и наименьших конечных значений каждого подинтервала соответственно. Значения сумм сходятся, когда подинтервалы уменьшаются вдвое от верхнего левого угла до нижнего правого. Это есть верхняя (нижняя) сумма Дарбу (метод Дарбу-Римана).

Обобщенные алгоритмы методов

Метод прямоугольников

В качестве метода прямоугольников можно воспользоваться методом Дарбу-Римана. Алгоритм метода Дарбу-Римана на каждом шаге вычисляются две суммы – верхняя (S2) и нижняя (S1):

f1 = f(x);              // значение функции на левой границе отрезка
f2 = f(x + dx);         // значение функции на правой границе отрезка
if (f1 <= f2)           // возрастающий участок
{
    S1 += f1 * dx;      // нижняя сумма
    S2 += f2 * dx;      // верхняя сумма 
}
else                    // убывающий участок
{
    S2 += f1 * dx;      // верхняя сумма 
    S1 += f2 * dx;      // нижняя сумма 
}

Вычисления прекращаются, если | S2 - S1 | < eps.

к сведению

Обратите внимание, что данный алгоритм представлен лишь в качестве примера, иллюстрирующего принцип работы одного из варианта метода прямоугольников. Указанный здесь критерий точности не является критерием точности, который необходимо использовать в программе. При реализации программы необходимо использовать правило Рунге (см. дальше). В связи с этим, значение интеграла методом прямоугольников необходимо искать по одной из формул: левых, правых или средних прямоугольников.

Метод трапеций

Алгоритм метода трапеций аналогичен алгоритму метода прямоугольников, только площадь элементарной трапеции вычисляется по формуле:

$$S_t = dx*(f(x)+f(x+dx))/2$$

При этом значения функций на границах внутренних отрезков при вычислении интеграла используются дважды, а на границах интервала $[a, b]$ - только один раз.

Задача вычисления определенного интеграла

Задача вычисления определенного интеграла формулируется следующим образом: вычислить $\int_{a}^{b} f(x) \,dx$ для подынтегральной функции $f(x)$ при заданных значениях пределов интегрирования $a$, $b$ и требуемой точности $eps$.

При численном интегрировании площадь под кривой заменяется суммой площадей "элементарных" прямоугольников с высотой, проведенной из середины основания.

Формула приближенного значения определенного интеграла представляется в виде

$$S =\sum\limits_{i=1}^N f(x_i) \Delta x ,$$

где:

• $x_i = a + \Delta x / 2 + (i-1) \Delta x$;
• $N$ - число элементарных прямоугольников.

Для уменьшения объема вычислений множитель $\Delta x$ следует вынести за знак суммы. Тогда в цикле нужно выполнять только суммирование, а затем полученную сумму один раз умножить на $\Delta x$.

Оценка погрешности

Для оценки погрешности вычисления интеграла на практике используют правило Рунге. Суть правила состоит в том, что выполняют вычисление интеграла с двумя разными шагами изменения переменной $x$, а затем сравнивают результаты и получают оценку точности. Наиболее часто используемое правило связано с вычислением интеграла дважды: с шагом $\Delta x$ и шагом $\Delta x / 2$.

Для методов прямоугольников и трапеций погрешность $R_{\Delta x/2}$ вычисления интеграла с шагом $\Delta x / 2$ оценивается следующей формулой:

$$|R_{\Delta x/2}| = \cfrac{|I_{\Delta x/2} - I_{\Delta x}|}{3} ,\quad (1)$$

где:

• $I_{\Delta x/2}$ – значение интеграла, вычисленное с шагом $\Delta x/2$;
• $I_{\Delta x}$ – значение интеграла, вычисленное с шагом $\Delta x$.

В программе вычисления интеграла с точностью eps во внутреннем цикле находят значение определенного интеграла с шагом $\Delta x/2$. Во внешнем цикле производится сравнение значений интегралов, вычисленных с шагами $\Delta x$ и $\Delta x/2$ соответственно. Если требуемая точность не достигнута, то число разбиений удваивается, а в качестве предыдущего значения интеграла берут текущее и вычисление интеграла выполняется при новом числе разбиений.

Сигнатуры функций

осторожно

Один из аргументов функций IntRect и IntTrap должен быть указатель на функцию $f$, вычисляющая значение одной из четырех приведенных выше функций.

Чтобы передать внутрь функции указатель на функцию, см. статью "Указатели на функции как параметры и результаты функций".

Функция IntRect

Вычисление интеграла оформить в виде функции IntRect, формальными параметрами которой являются:

• f – имя интегрируемой функции;
• a, b – границы интервала интегрирования;
• eps – требуемая точность;
• n – число прямоугольников, при котором достигнута требуемая точность (выходной).

Функция возвращает значение интеграла.

Прототип функции:

double IntRect(TPF f, double a, double b, double eps, int* n);

Здесь TPF – тип указателя на подынтегральную функцию:

typedef double (*TPF)(double);

Для хранения и печати результатов вычислений используйте структуру, элементами которой являются:

• наименование функции;
• значения интеграла (точное и вычисленное в виде суммы);
• число "элементарных" прямоугольников n, при котором достигнута требуемая точность.

Точные значения, полученные аналитически, нужны для оценки правильности результатов численного интегрирования.

к сведению

Так как в лабораторной работе требуется выполнять вычисление интеграла для четырех функций, для пяти значений точности для каждой функции и двумя методами, то для сокращения объема программы следует использовать циклы, а для обеспечения возможности реализации циклов обрабатываемые данные нужно хранить в массивах (массив указателей на функции, массив значений точности, массив структур для хранения и печати результатов вычислений).

Функция IntTrap

Прототип функции:

double IntTrap(TPF f, double a, double b, double eps, int* n);

Формулы для вычисления точных значений интеграла

• $\int_{a}^{b} x \,dx$ = (b*b - a*a)/2.0
• $\int_{a}^{b} sin(22x) \,dx$ = (cos(a*22.0) - cos(b*22.0))/22.0
• $\int_{a}^{b} x^4 \,dx$ = (b*b*b*b*b - a*a*a*a*a)/5.0
• $\int_{a}^{b} \arctan(x) \,dx$ = b*atan(b) - a*atan(a) - (log(b*b+1) - log(a*a+1))/2.0

Проверка задания

Подготовленная программа для решения задания проверяется вручную преподавателем (визуальный контроль).

Методический материал

1. Требования к отчету
2. Функция для печати таблицы результатов:
   1. Для программ на C
   2. Для программ на C++
3. Динамические массивы:
   1. Для программ на C
   2. Для программ на C++
4. Контрольные вопросы:
   1. Для потока на С
   2. Для потока на С++